스프레드 시트 데이터 분석 2 - 평균비교(t-test)
오늘은 스프레드 시트를 통해서 t-test를 하는 법에 대해서 알아보도록 하겠습니다.
t-test는 무엇인가요?
두 집단 간 평균을 비교하는 대표적인 방법입니다.
t-test는 분석을 위해서 여러 가지 가정을 하게 됩니다.
1. 두 집단의 분포가 정규분포이다.(정규성)
2. 두 집단의 분포는 같은 분산을 가지고 있다(등분 산성)
3. 실험은 서로 독립적으로 이루어졌을 것이다.(독립성)
안타깝지만 해당 가설은 스프레드시트로 검증하기가 어렵습니다. 하지만 R로는 쉬우니 한번 확인해보시기 바랍니다.
https://kbkb456.tistory.com/93?category=915378
R 프로그래밍 10 - T-TEST(독립표본 t-test)
https://kbkb456.tistory.com/90 R 프로그래밍 9 - dplyr을 활용하여 깔끔한 코드로 데이터 전처리하기(filter, arrange, mutate, select, summa https://kbkb456.tistory.com/62 R 프로그래밍 8 - R 데이터 프레..
kbkb456.tistory.com
이전에 R에서 t-test 하는 법에 포스팅을 적은 적이 있습니다. (자세한 설명도 이안에 있습니다!)
어떻게 사용하나요?
구문
TTEST(범위1, 범위2, 꼬리, 유형)
범위 1 - 첫 번째 t-검정의 대상으로 데이터 리스트
범위 2 - 두 번째 t-검정의 대상으로 데이터 리스트
꼬리 - 단측 및 양측 분포를 활용할지 결정
1: 단측 분포를 사용
2: 양측 분포를 사용
유형 - t-검정의 유형을 지정
1: 대응 샘플 테스트 수행
2: 두 샘플의 등분산 테스트 수행
3: 두 샘플의 이분산 테스트 수행
사용 예시
만약 치킨 프랜차이즈의 지역별 판매량에 대한 데이터가 있다고 가정해 봅시다.
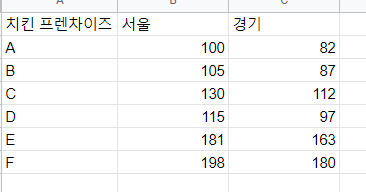
이런 가설이 나올 수 있습니다.
H0: 치킨 프렌차이즈의 두 지역 간 판매량 차이는 없을 것이다.
H1: 판매량 차이는 있을 것이다.
그리고 이에 대해 검정방법은 P-value 0.05하에서 양측검정 + 등분산 테스트로 진행해보도록 하겠습니다.
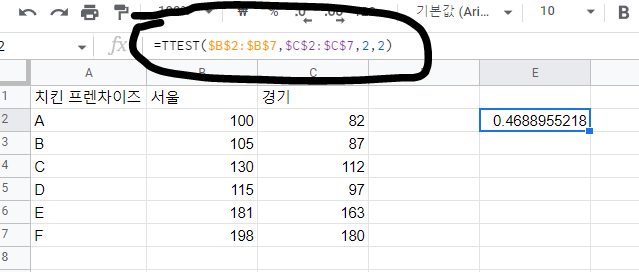
p-value는 0.46으로 0.05하에서 대립 가설을 기각하고 귀무가설을 채택 치킨 프랜차이즈의 지역별 판매량 차이는 통계적으로 없다고 결론을 내릴 수 있습니다.
데이터가 평균적으로 애매한 차이를 보일 때 자주 쓰는 분석으로 알고 있으면 도움이 됩니다.